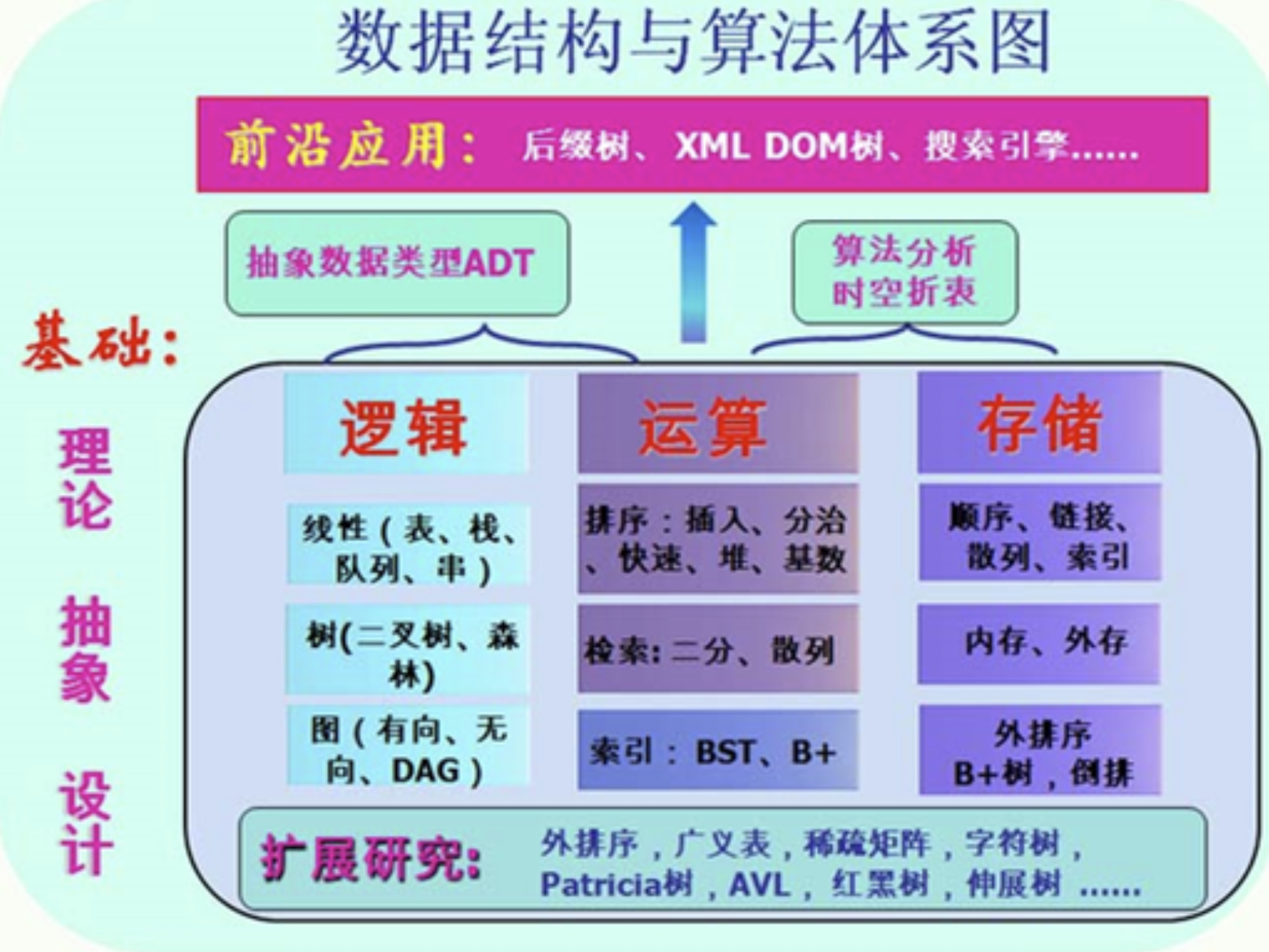
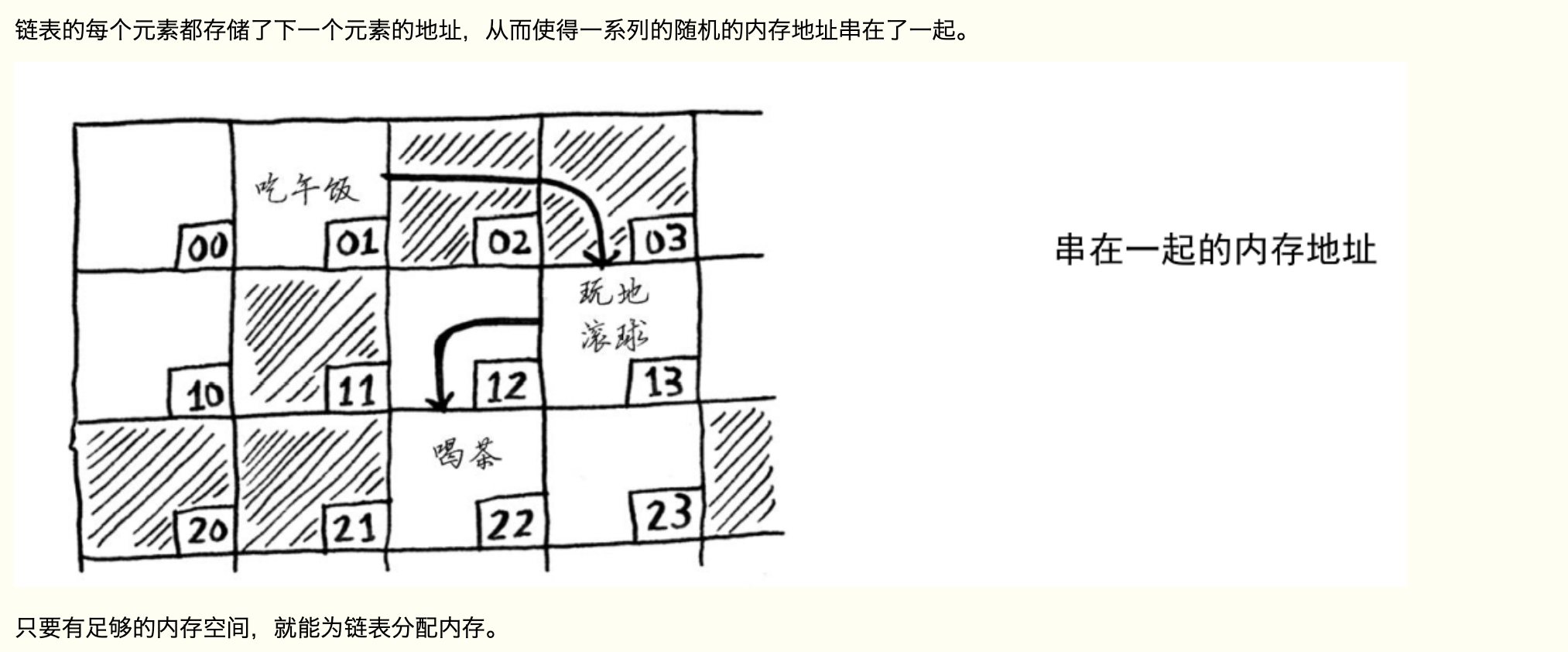
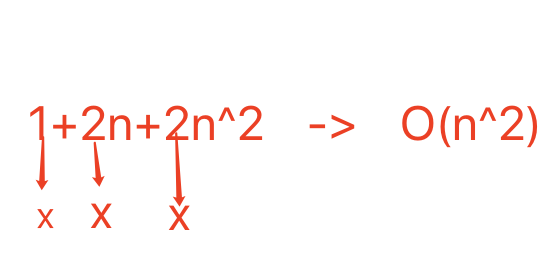# 数据结构与算法
数据结构和算法是程序员的基本功,值得每一个程序员好好学习。数据结构表示计算机存储数据的方式,算法是完成某个特定任务的过程。
# 什么是数据结构
数据结构起源于程序设计,是用计算机来存储、组织数据的方式。数据结 构不是使我们学会编码,而是为我们提供一种编程的思想,具有更好的思路。
- 广义的说法:数据结构 = 数据存储 + 算法
- 狭义的说法:数据结构 = 数据的存储;
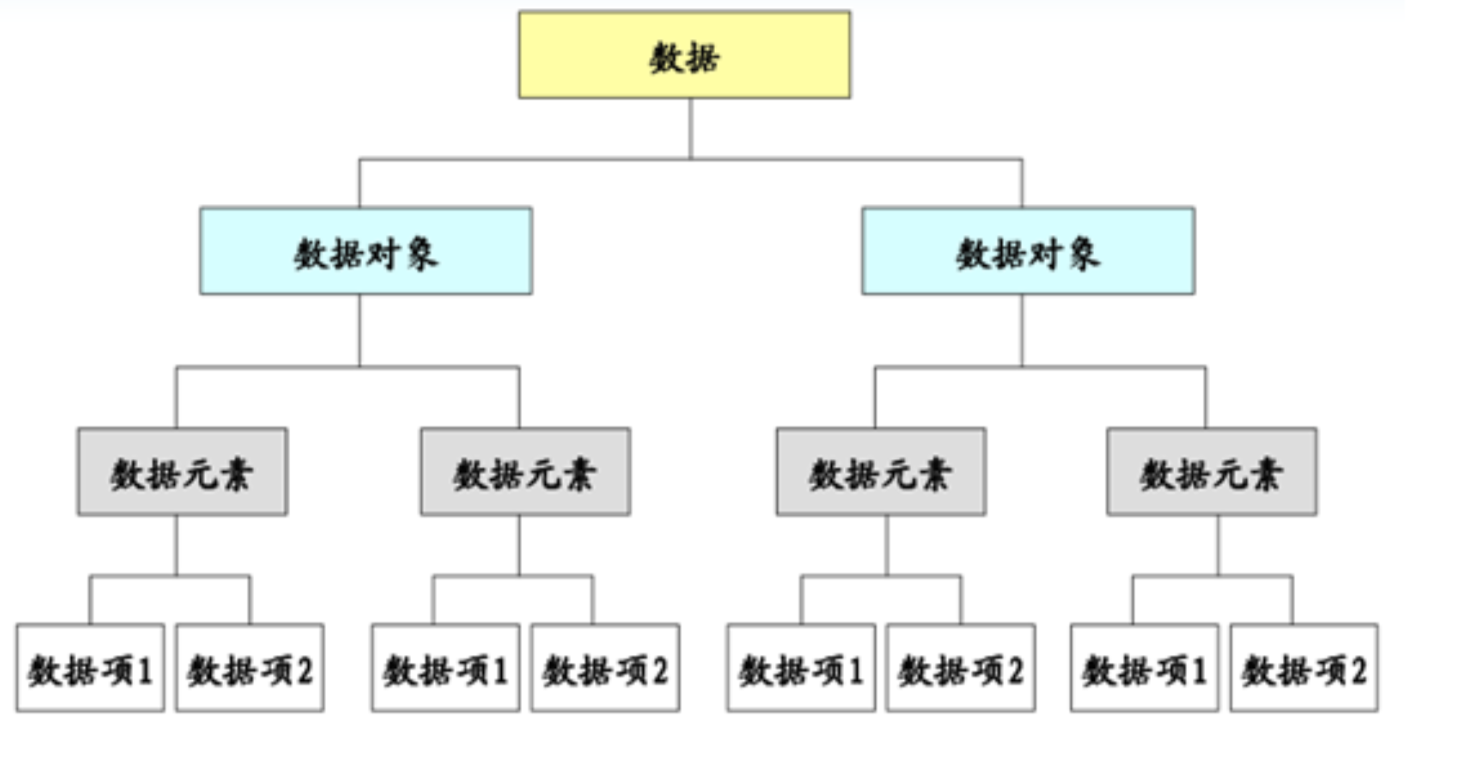
# 数据结构中的概念
- 数据:统称
- 数据元素:相当于是视频文件
- 数据项:相当于视频的每一帧
- 数据对象:相当于像素点
- 数据结构:数据元素相互之间
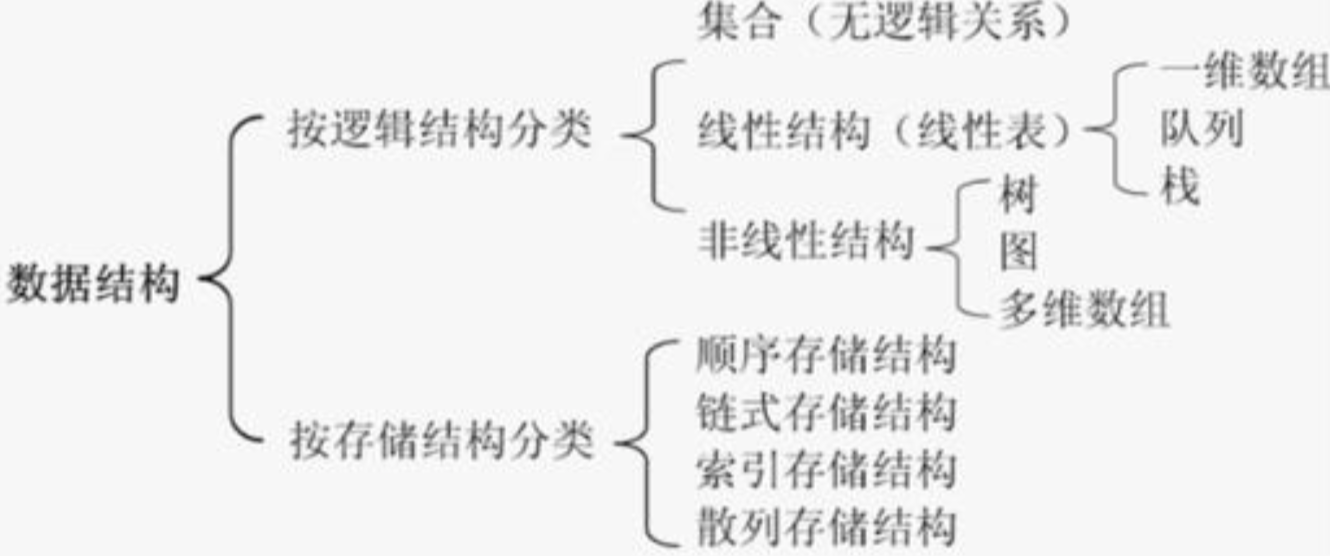
# 数据结构分类
在计算机科学中,数据结构(data structure)是计算机中存储、组织数据的方式。通常我们可以从逻辑结构和存储结构这两个维度进行分类。
- 逻辑结构:反映数据元素之间的逻辑关系。在设计层面上讲,是面向问题的;
- 存储结构:数据结构在计算机中的表示。在实现层面上讲,面向计算机的,其基本的目标就是将数据及其逻辑关系存储到计算机的内存中;
# 按逻辑结构分类
集合(无逻辑关系)
线性结构(线性表)
- 一维数组。
- 队列。
- 栈。 数据结构中的元素存在一对一的相互关系;打个比方,我要高考了,但是我数学不好,所以我请了一个数学老师给我单独补课,并且规定在我补课期间,该数学老师不能跟其他人补课,那么我和这个数学老师就是一对一的关系,我们之间的关系就是他跟我补课。还比如排队,每列只站一个人,每列总共十个人,那么他们每个人之间有先后关系,但是都是一对一的先后关系。像内存就属于线性结构。他可以使用一元一次方程表示,是连续的,而且前后石油依赖关系的,前后只能一个
非线性结构。
- 树。 数据结构中的元素存在一对多的相互关系;比如,一个数学老师给两个或者多个学生补课,那么老师和学生之间就是一对多的关系。
- 图。
数据结构中的元素存在多对多的相互关系。
比如我们的交通网,长沙有n条高速公路到达上海,同时上海也有k条高速公路到达长沙,长沙到上海是一对三n的关系,上海到长沙也是一对k的关系,所以长沙和上海是多对多的关系。
- 多维数组。
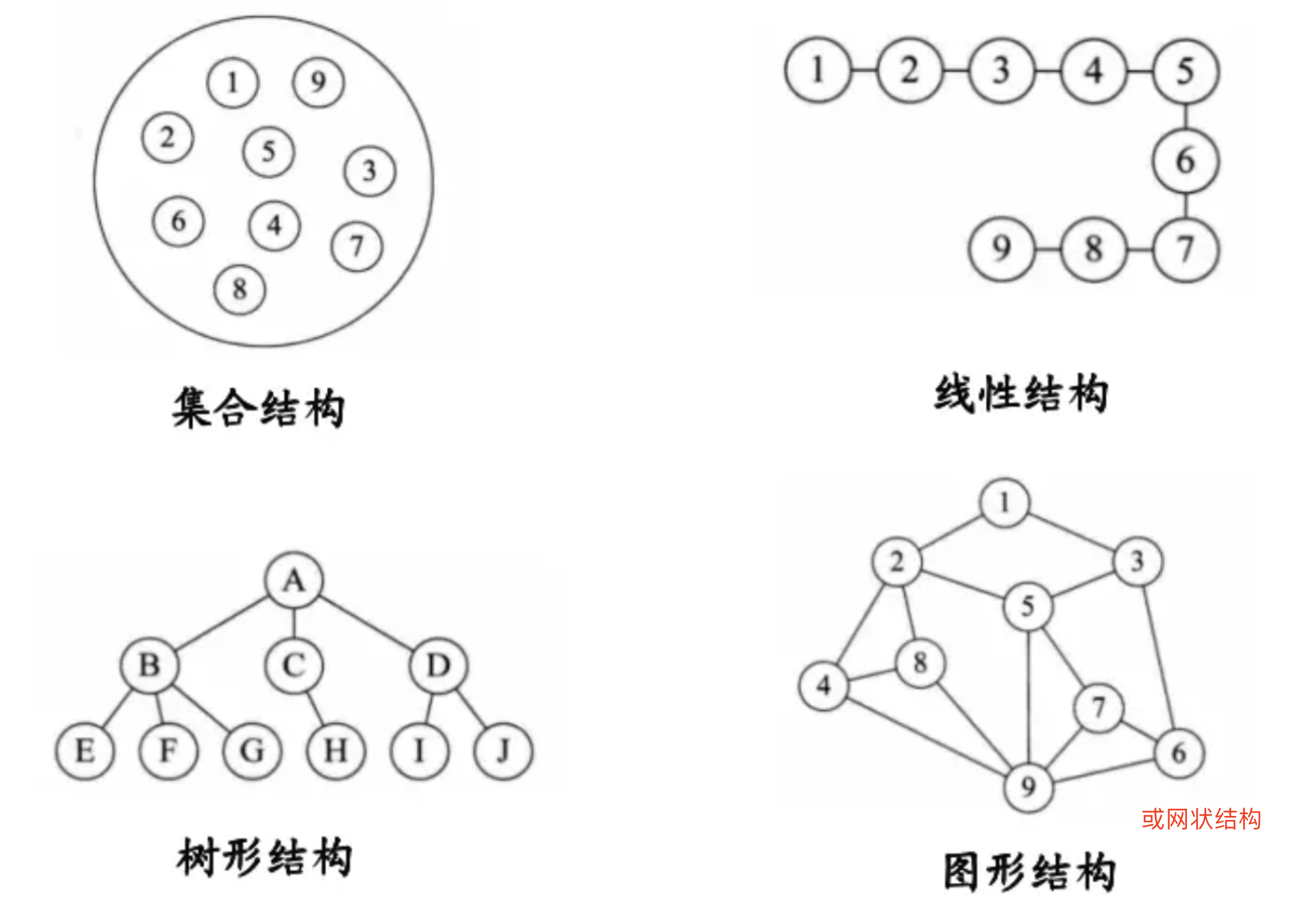
# 集合
数据结构中的集合关系就类似于数学中的集合。
- 集合中的数据成员是无序的。
- 每个数据成员在集合中不能重复,仅且只出现一次。
例子:数据结构中的元素之间除了“同属一个集合” 的相互关系外,别无其他关系。打个比方,我有一个篮子,篮子里面放了一个苹果,一个香蕉,一个梨子。这三种水果除了放在一个篮子里面,他们没有其它联系。这篮子里三种水果就属于一个集合,他们老死不相往来。JS中的Set其实就是一种集合。
# 线性结构
线性结构中的数据元素之间是一对一的关系。也就是数据元素一个连接一个 地排列。
- 用来存放特定的某一个类型的元素
- 物理结构为顺序表(原生数组)和链表(数据在内存中表示)
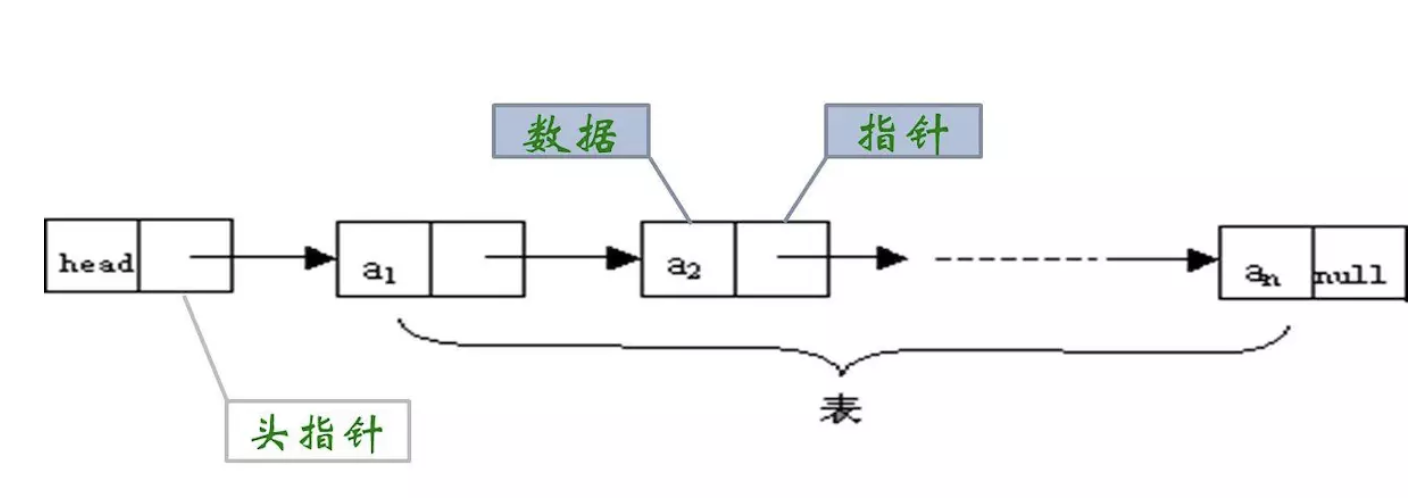
线性表
对于线性表来说,第一个元素叫首元素,最后一个元素叫尾元素,除了首元素与尾元素外,中间的元素前边都有一个元素,叫前驱元素,后边也有一个元素叫后继元素,尾元素只有后继元素,首元素只有前驱元素。
注意⚠️:Array可能是顺序表也可能是链表,链表维护是动态的,需要多大申请多大内存
线性表的一些操作
- 可以对线性表进行创建、添加、删除、查找,遍历、读、销毁线性表
链表
线性表优点:
- 插入删除速度快(因为有next指针指向其下一个节点,通过改变指针的指向可以方便的增加删除元素)
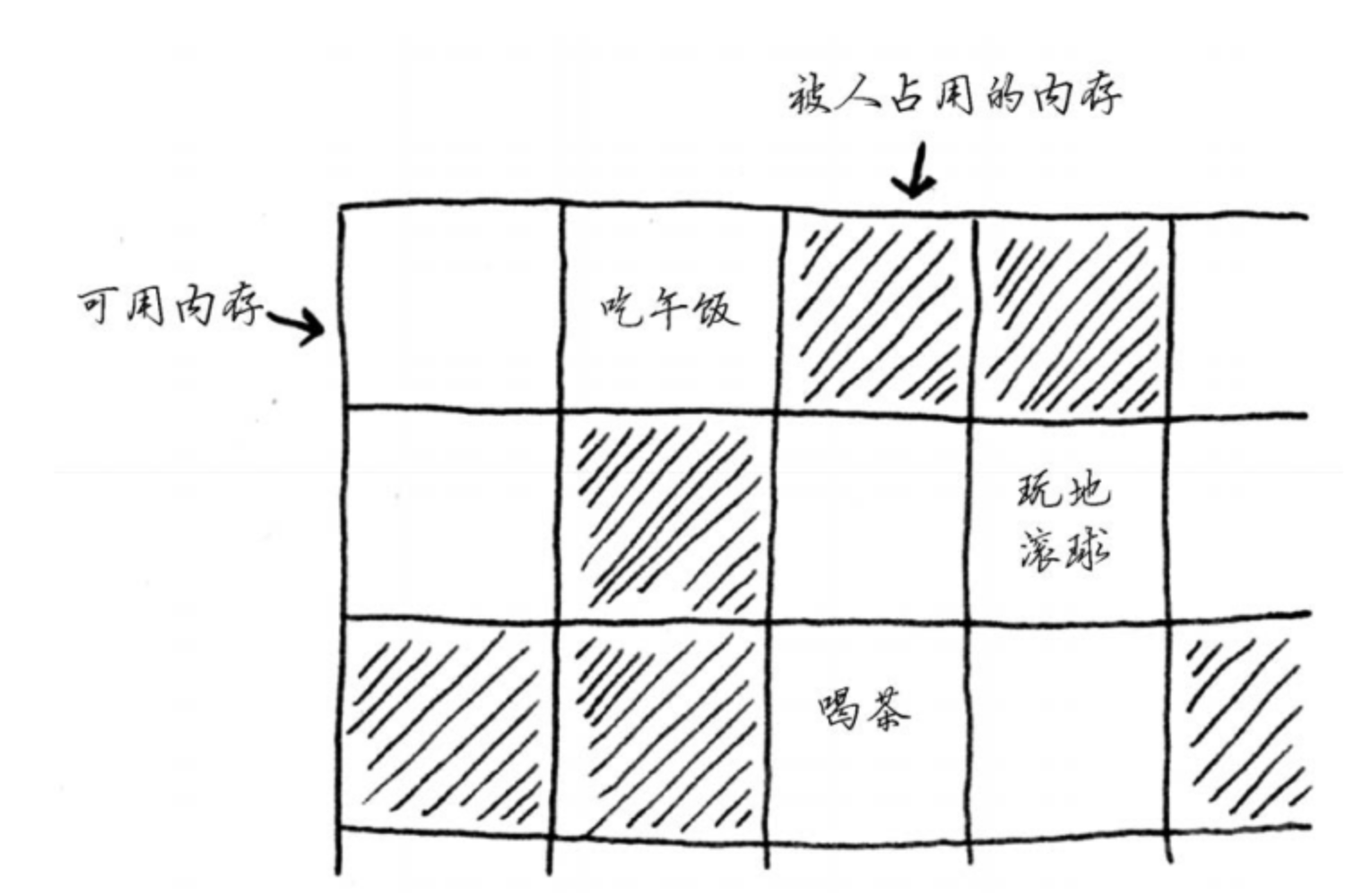
- 内存利用率高,不会浪费内存(可以使用内存中细小的不连续空间(大于node节点的大小),并且在需要空间的时候才创建空间)
- 大小没有固定,拓展很灵活。
线性表缺点:
- 不能随机查找,必须从第一个开始遍历,查找效率低
一维数组
特点:
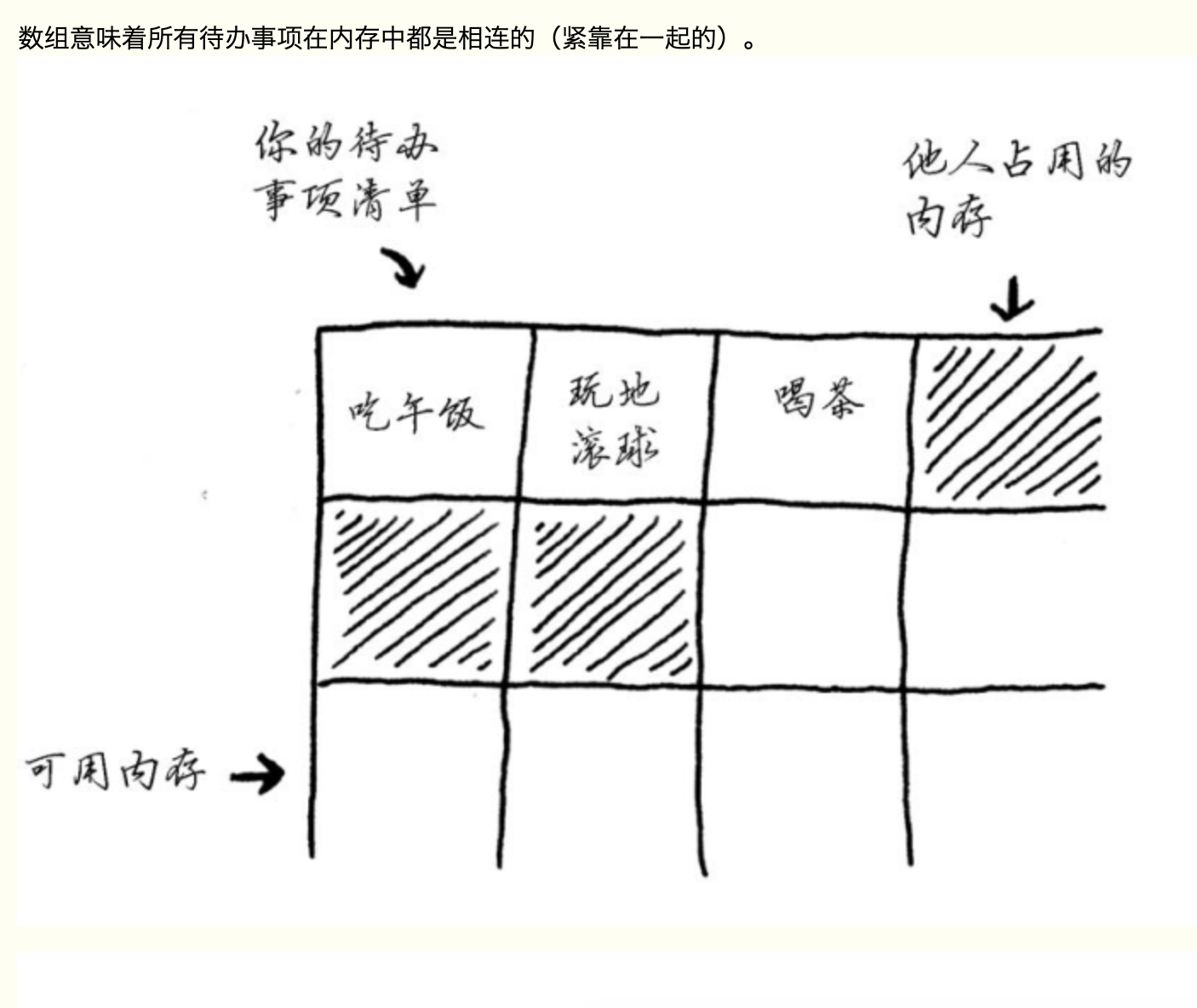
- 1.静态分配内存(固定需要向内存申请的位置,而且需要给预留位置,这样可能出现:你额外请求的位置可能根本用不上,这将浪费内存。你没有使用,别人也用不了。)
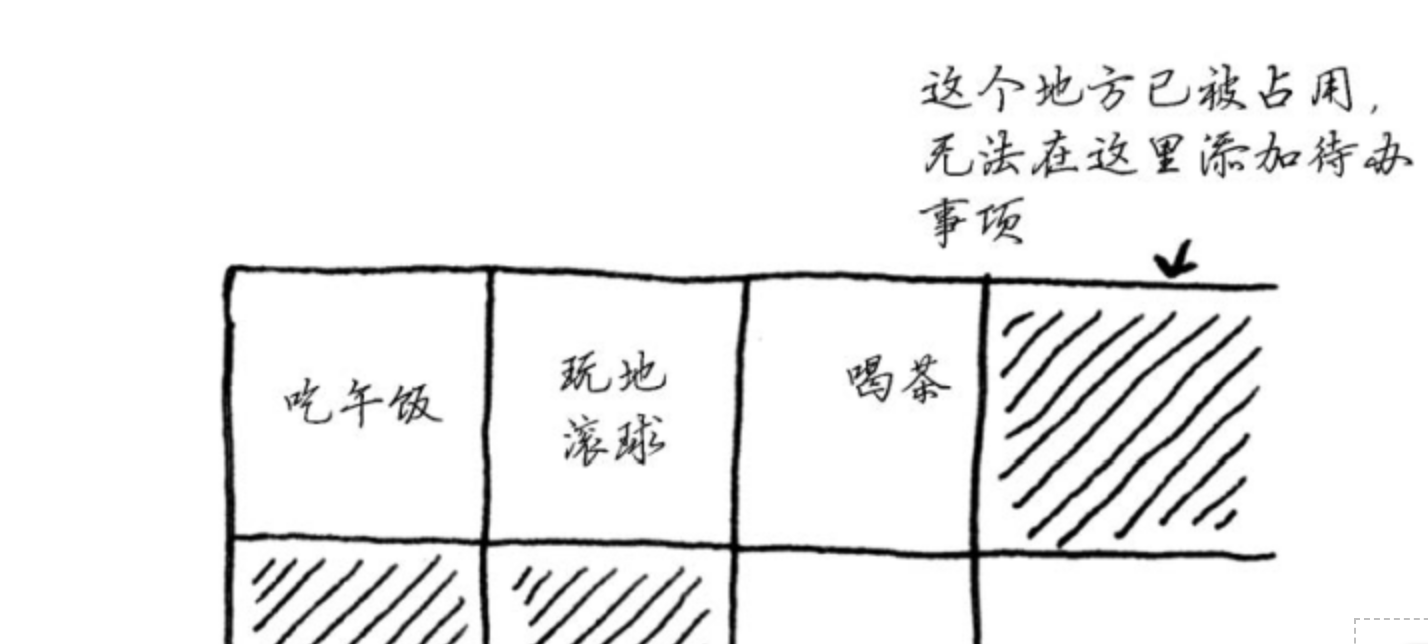
- 2.在内存中连续(当需要添加元素的时候,如果申请的位置占满了,就需要转移)
- 3.查找快,数组利用下标定位,时间复杂度为O(1)
- 4.数组插入或删除元素的时间复杂度O(n)(删除时必须要将后面的元素都向前移动,插入时必须将后面的元素都向后移动。如果空间不足,还要重新复制新的空间。)
以下来自算法图解
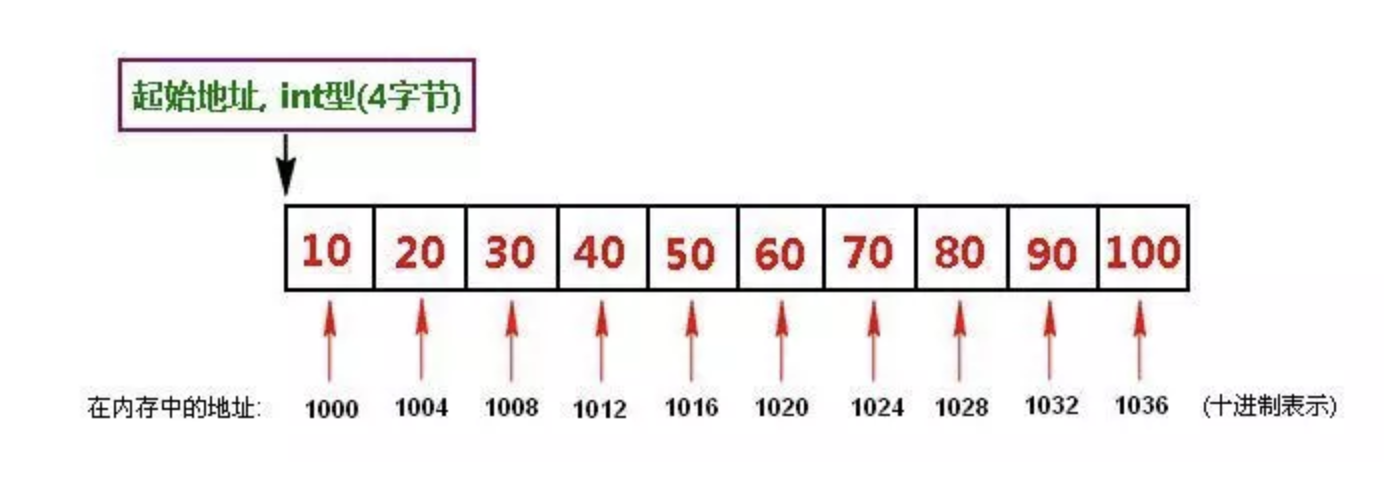
优势:
数组,则很方便读取每一个元素的内容。因为知道第一个,就知道了所有的地址。它们是连在一起的。
链表
特点:
- 1.动态分配内存
- 2.在内存中是不连续的(内存利用率高,不会浪费内存(可以使用内存中细小的不连续空间(大于node节点的大小),并且在需要空间的时候才创建空间)
- 3.链表定位元素
- 4.大小没有固定,拓展很灵活。
缺点:
不能随机查找,必须从第一个开始遍历,查找效率低
链表插入元素只需要修改它前面的那个元素指向的地址就可以了。
链表删除元素也是只需要修改它前面的那个元素指向的地址就可以了。
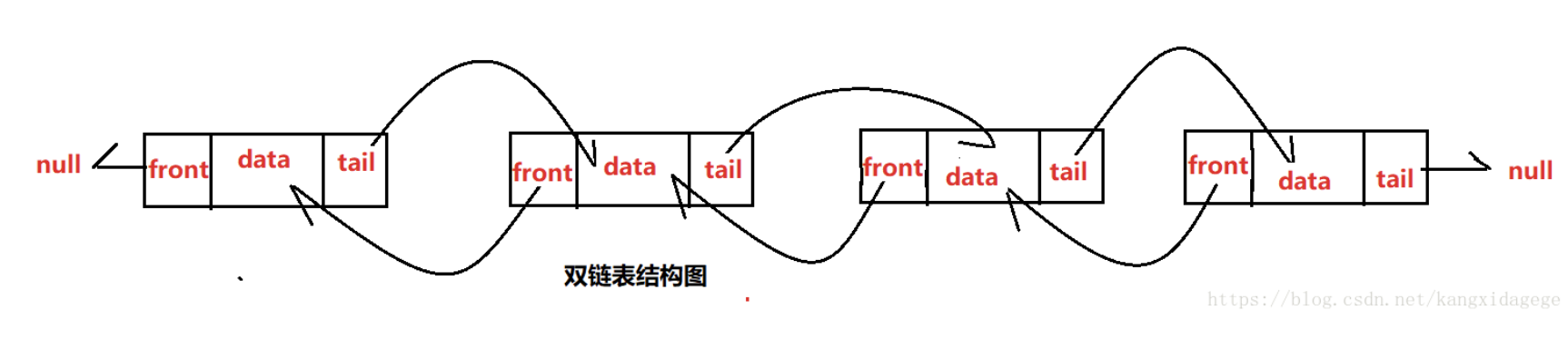
分类:链表分为单向链表和双向链表,
单链表与双链表的结构图如下:
只能朝一个方向进行遍历(接着后继元素一个一个的遍历,结构相对简单只有后继指针,操作时只需要断一个)
可以从俩个方向遍历,因为有俩个指针,操作起来麻烦,需要操作俩次
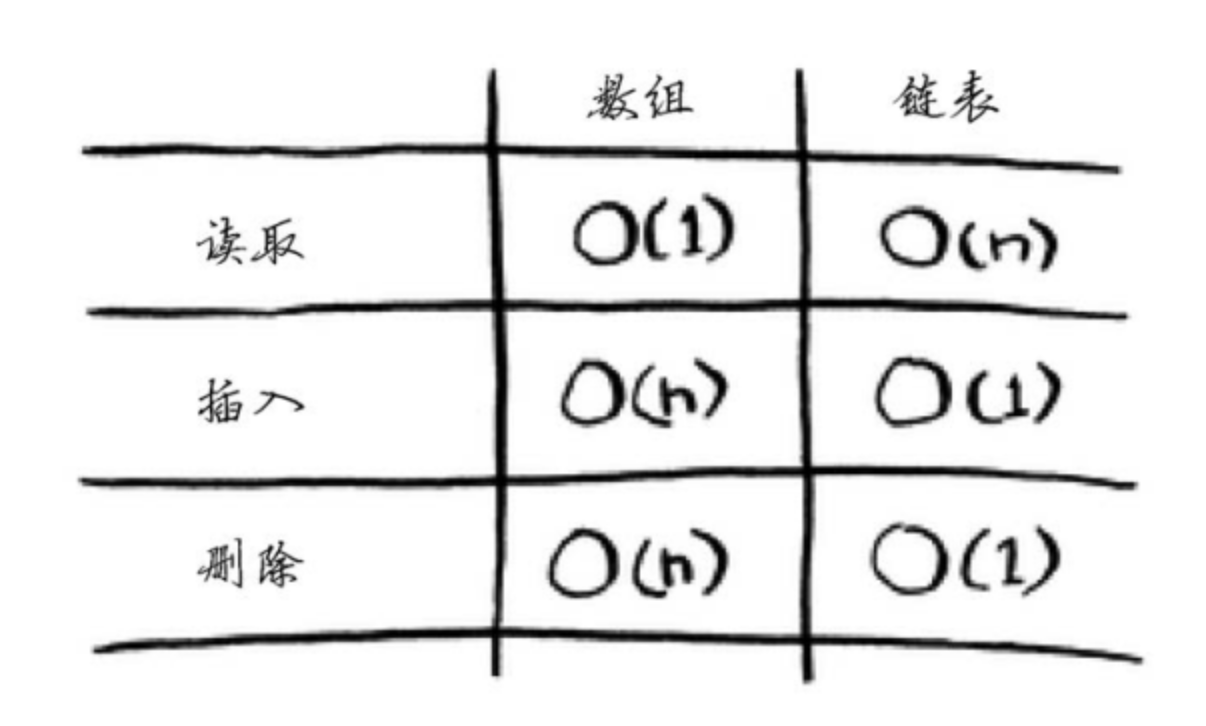
数组与链表时间复杂度比较
一些常见的问题
为什么市面上单链表应用比多链表应用广泛一些呢?
在时间复杂度上来考虑,如果进行查询的话,双链表可以通过二分法查找(从首尾元素开始遍历),时间复杂度是log(n)而单链表只能朝一个方向遍历所以时间复杂度n,事实证明双链表的时间复杂度低,但是双链表每个节点都会比单链表多一个指针(这个指针的length在32位系统中是4字节,在64位系统中是8个字节),占用空间也就大了,这时设计者就会采用以时间换空间的做法,这时一种工程总体上的衡量。
总结:
插入删除多,读取少。用链表。
插入删除少,读取多。用数组。
接下来我们看一下线性结构的衍生结构
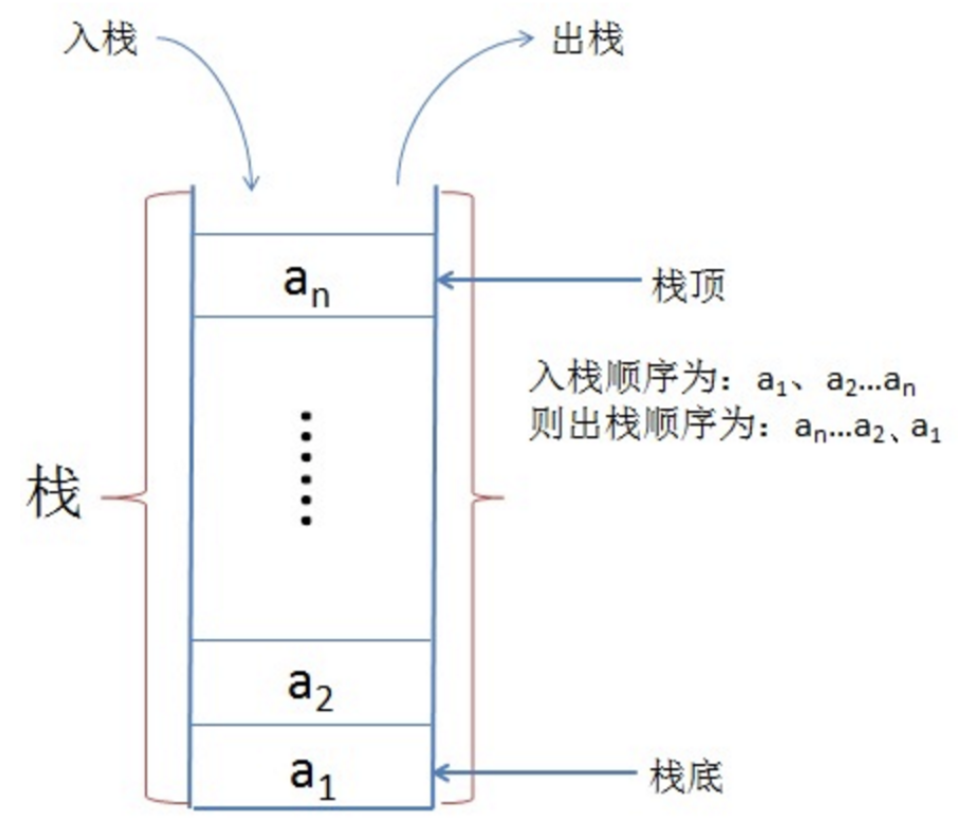
# 栈
- 栈是一种只在一端进行删除、插入操作的线性表
- 栈顶进行删除、插入的一端
- 栈底不能进行删除、插入的那一端
- 栈是一种先入后出表、LIFO(Last In First Out)
# 栈的几种操作
其实也是一个栈的生命周期
- 1.创建栈结构(空栈):没有东西的栈(这个时候栈顶就是栈底)
- 2.进栈:在栈顶压入元素(只压一个元素,这个时候栈顶就是栈底)
- 3.退栈:删除或弹出栈顶的元素
- 4.读取栈顶:只看看栈顶的东西,不拿,相当与你舔一舔(有点邪恶了。。)
- 5.清空栈
- 6.销毁栈
# 栈的实现
普通的栈常用的有以下几个方法:
push 添加一个(或几个)新元素到栈顶
pop 溢出栈顶元素,同时返回被移除的元素
peek 返回栈顶元素,不对栈做修改
isEmpty 栈内无元素返回 true,否则返回 false
size 返回栈内元素个数
clear 清空栈
class Stack {
constructor(){
this._items = [];创建一个栈结构
}
//向栈内压入一个元素
push(item){
this._items.push(item)
}
//把栈顶的元素弹出
pop(){
return this._items.pop()
}
//返回栈顶元素
peek(){
return this.items[this.items.length-1]
}
//判断栈是否为空
isEmpty(){
return !this._item.length
}
//栈的个数
size(){
return !this._item.length
}
//清空栈
clear(){
this.item = []
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 栈应用
下边举几个例子:
1.解决括号匹配检查:检查html标签是否闭合或者简单点就是检查js里括号有没有闭合,具体过程就是查到左括号入栈,查到右括号出栈,最后的结果应该是空栈。
2.浏览器的后退或编辑器的undo功能
3.(1)十进制转任意进制
要求:给定一个函数,输入目标数值和进制基数,输出对应的进制数(最大为16进制)
baseConverter(10, 2) ==> 1010
baseConverter(30, 16) ==> 1E
2
分析:进制转换的本质——将目标值一次一次除以进制基数,得到的取整值为新目标值,记录下余数,直到目标值小于0,最后将余数逆序组合即可。利用栈,记录余数入栈,组合时出栈。
// 进制转换
function baseConverter(delNumber, base) {
const stack = new Stack();
let rem = null;
let ret = [];
// 十六进制中需要依次对应A~F
const digits = '0123456789ABCDEF';
while (delNumber > 0) {
rem = Math.floor(delNumber % base);
stack.push(rem);
delNumber = Math.floor(delNumber / base);
}
while (!stack.isEmpty()) {
ret.push(digits[stack.pop()]);
}
return ret.join('');
}
console.log(baseConverter(100345, 2)); //输出11000011111111001
console.log(baseConverter(100345, 8)); //输出303771
console.log(baseConverter(100345, 16)); //输出187F9
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 4.利用普通栈实现一个有 min方法的栈
思路: 使用两个栈来存储数据,其中一个命名为 dataStack,专门用来存储数据,另一个命名为 minStack,专门用来存储栈里最小的数据。始终保持两个栈中的元素个数相同,压栈时判别压入的元素与 minStack栈顶元素比较大小,如果比栈顶元素小,则直接入栈,否则复制栈顶元素入栈;弹出栈顶时,两者均弹出即可。这样 minStack的栈顶元素始终为最小值。
lass MinStack {
constructor() {
this._dataStack = new Stack();
this._minStack = new Stack();
}
push(item) {
this._dataStack.push(item);
// 为空或入栈元素小于栈顶元素,直接压入该元素
if (this._minStack.isEmpty() || this._minStack.peek() > item) {
this._minStack.push(item);
} else {
this._minStack.push(this._minStack.peek());
}
}
pop() {
this._dataStack.pop();
return this._minStack.pop();
}
min() {
return this._minStack.peek();
}
}
const minstack = new MinStack();
minstack.push(3);
minstack.push(4);
minstack.push(8);
console.log(minstack.min()); // 3
minstack.push(2);
console.log(minstack.min()); // 2
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
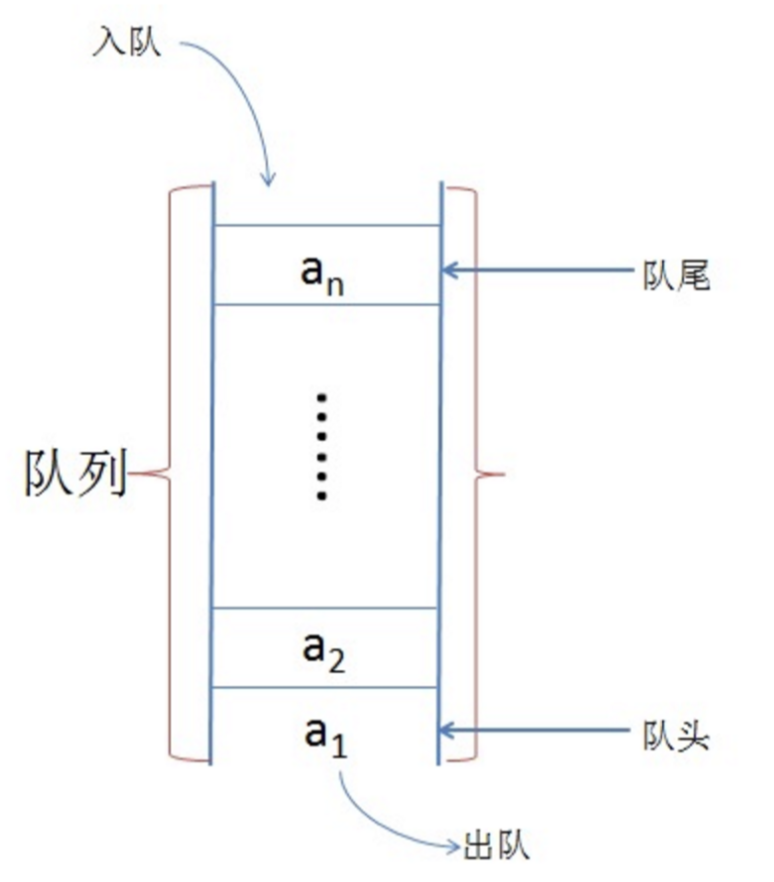
# 队列
- 队列是一种只允许在表的一端进行插入,而在另一端删除的线性表
- 队头:允许删除的一端
- 队尾:允许插入的一端先进先出表
队列是一种先入先出表、FIFO(First In First Out)
# 队列的几种操作
其实也是一个队列的生命周期
- 创建一个空队列
- 判断队列是否是空队列
- 入队:往队列中插入元素
- 出队:从队列中删除元素
- 求队列头部的值
注意⚠️
- 队尾的位置一直在变
- 只有一个元素的队列或者空队列队头就是队尾。
- 有急事的元素可以优先出队列,这是一个可以插队的队列叫
优先队列 - 环形队列:无队头与队尾,需要指定,最好用链式结构实现,用顺序表结构也可以实现,但是维护起来麻烦,因为队头队尾一直在变。
# 队列的实现
普通的队列常用的有以下几个方法:
- enqueue 向队列尾部添加一个(或多个)新的项
- dequeue 移除队列的第一(即排在队列最前面的)项,并返回被移除的元素
- head 返回队列第一个元素,队列不做任何变动
- tail 返回队列最后一个元素,队列不做任何变动
- isEmpty 队列内无元素返回 true,否则返回 false
- size 返回队列内元素个数
- clear 清空队列
class Queue {
constructor() {
this._items = [];
}
enqueue(item) {
this._items.push(item);
}
dequeue() {
return this._items.shift();
}
head() {
return this._items[0];
}
tail() {
return this._items[this._items.length - 1];
}
isEmpty() {
return !this._items.length;
}
size() {
return this._items.length;
}
clear() {
this._items = [];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 队列的一些应用
- 排队
- 消息队列
- 任务队列
- 维护打印机任务
- 菲波那切数列(普通模式)
要求: 使用队列计算斐波那契数列的第n项。
分析: 斐波那契数列的前两项固定为1,后面的项为前两项之和,依次向后,这便是斐波那契数列。
function fibonacci(n) {
const queue = new Queue();
queue.enqueue(1);
queue.enqueue(1);
let index = 0;
while(index < n - 2) {
index += 1;
// 出队列一个元素
const delItem = queue.dequeue();
// 获取头部值
const headItem = queue.head();
const nextItem = delItem + headItem;
queue.enqueue(nextItem);
}
return queue.tail();
}
console.log(fibonacci(9)); // 34
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
- 用队列实现一个栈
要求: 用两个队列实现一个栈。
分析: 使用队列实现栈最主要的是在队列中找到栈顶元素并对其操作。具体的思路如下:
1.两个队列,一个备份队列 emptyQueue,一个是数据队列 dataQueue;
2.在确认栈顶时,依次 dequeue至备份队列,置换备份队列和数据队列的引用即可。
class QueueStack {
constructor() {
this.queue_1 = new Queue();
this.queue_2 = new Queue();
this._dataQueue = null; // 放数据的队列
this._emptyQueue = null; // 空队列,备份使用
}
// 确认哪个队列放数据,哪个队列做备份空队列
_initQueue() {
if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
this._dataQueue = this.queue_1;
this._emptyQueue = this.queue_2;
} else if (this.queue_1.isEmpty()) {
this._dataQueue = this.queue_2;
this._emptyQueue = this.queue_1;
} else {
this._dataQueue = this.queue_1;
this._emptyQueue = this.queue_2;
}
};
push(item) {
this.init_queue();
this._dataQueue.enqueue(item);
};
peek() {
this.init_queue();
return this._dataQueue.tail();
}
pop() {
this.init_queue();
while (this._dataQueue.size() > 1) {
this._emptyQueue.enqueue(this._dataQueue.dequeue());
}
return this._dataQueue.dequeue();
};
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
同样的,一个队列也能实现栈的基本功能:
class QueueStack {
constructor() {
this.queue_1 = new Queue();
this.queue_2 = new Queue();
this._dataQueue = null; // 放数据的队列
this._emptyQueue = null; // 空队列,备份使用
}
// 确认哪个队列放数据,哪个队列做备份空队列
_initQueue() {
if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
this._dataQueue = this.queue_1;
this._emptyQueue = this.queue_2;
} else if (this.queue_1.isEmpty()) {
this._dataQueue = this.queue_2;
this._emptyQueue = this.queue_1;
} else {
this._dataQueue = this.queue_1;
this._emptyQueue = this.queue_2;
}
};
push(item) {
this.init_queue();
this._dataQueue.enqueue(item);
};
peek() {
this.init_queue();
return this._dataQueue.tail();
}
pop() {
this.init_queue();
while (this._dataQueue.size() > 1) {
this._emptyQueue.enqueue(this._dataQueue.dequeue());
}
return this._dataQueue.dequeue();
};
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 串
stream(流)
# 树
# 基本概念
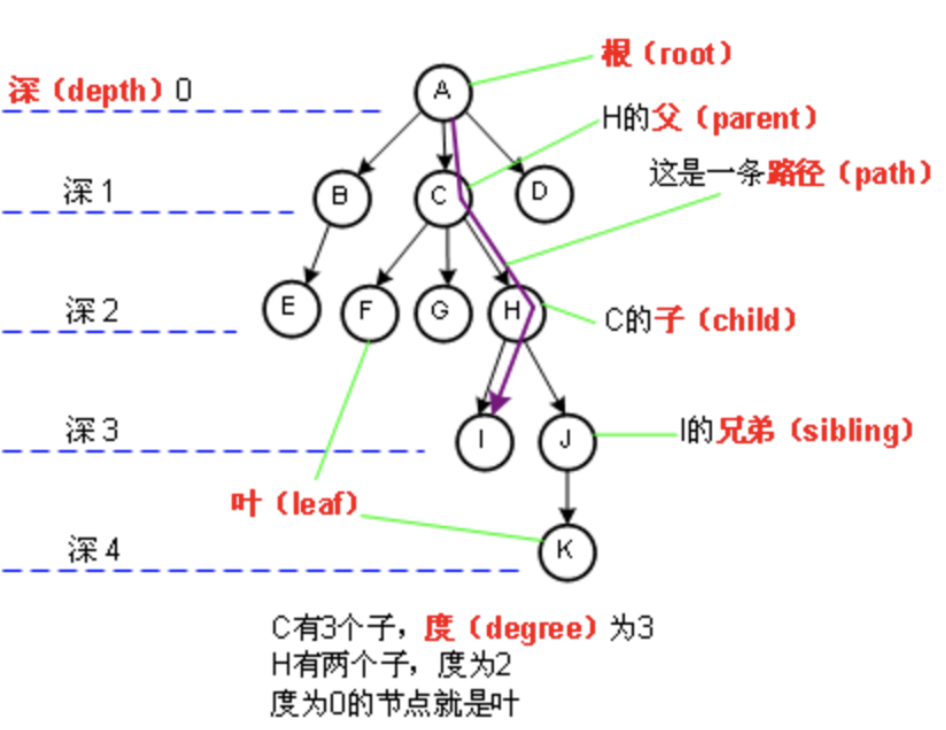
树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null或empty)树。一棵非空的树包括一个根结点,还(很可能)有多个附加结点,所有结点构成一个多级分层结构。简单点说他就是一个由若干个有限节点组成的一个具有层次关系的集合
他是一种操作效率比较高的的数据结构,是一个一对多的关系,和家谱一样
节点:树的每个元素;父节点:有子节点的节点是子节点的父节点根节点:最上边的父节点边或权:任意两个节点是被边连起来的;路径:任意两个节点是被边连起来的所有边组成路径;叶子节点:没有分叉的节点兄弟节点:兄弟节点的前提他们有一个共同的父节点度:有几个分叉就是几度,度为0的节点就是叶子节点深:有n层就是n-1深,如果只有一个节点深就为0熵:信息的混乱程度。文本格式较有序,好压,png就不好压
注意⚠️
- 一棵树中每两个点之间都有且只有一条路
- 有N个节点就有N-1条边
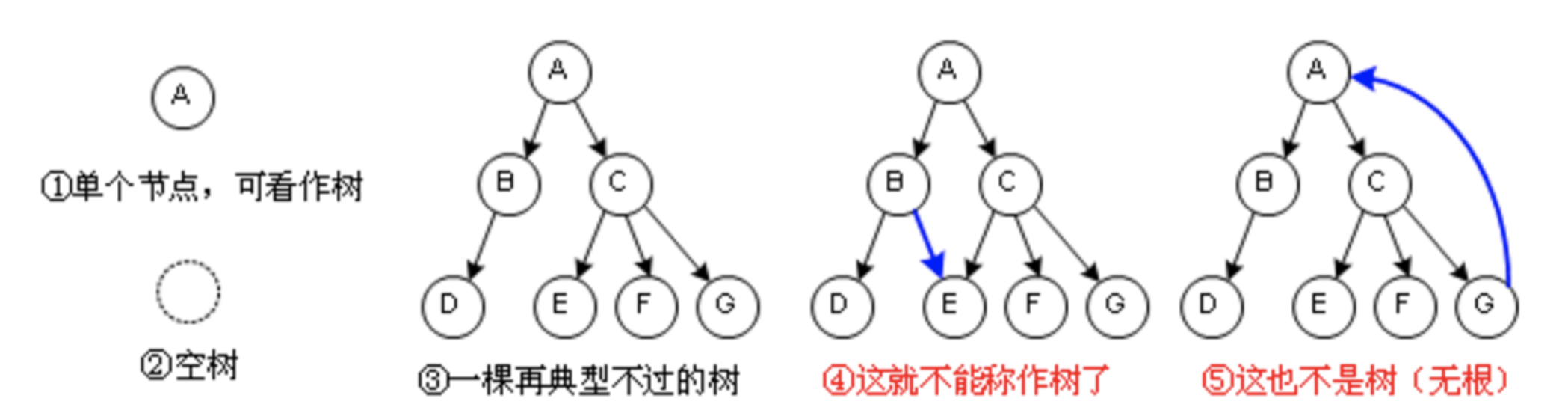
# 如何分辨是不是树
- 单个节点可以看成树;
- 可以有空树
- 树不能形成环路,形成环路就称为图了
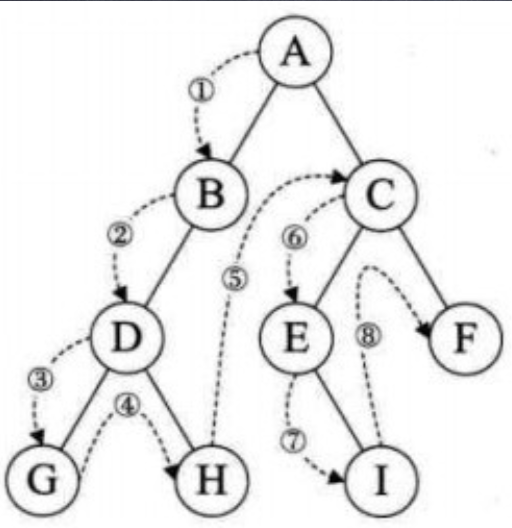
# 遍历树
按照某种规则,不重复地访问某种树的所有节点。我们可以分为
- 深度优先遍历
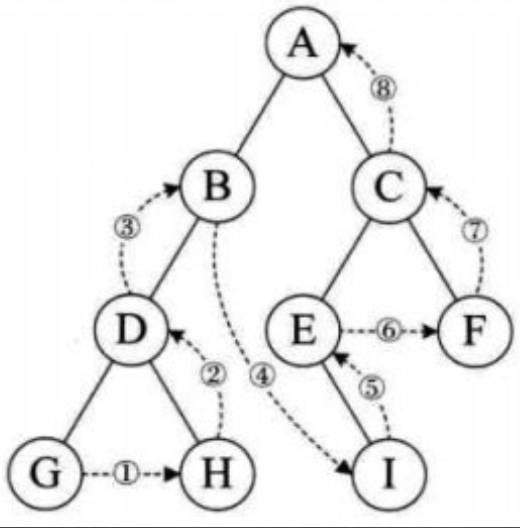
- 先序遍历(深度优先)
- 中序遍历(深度优先)
- 后序遍历(深度优先)
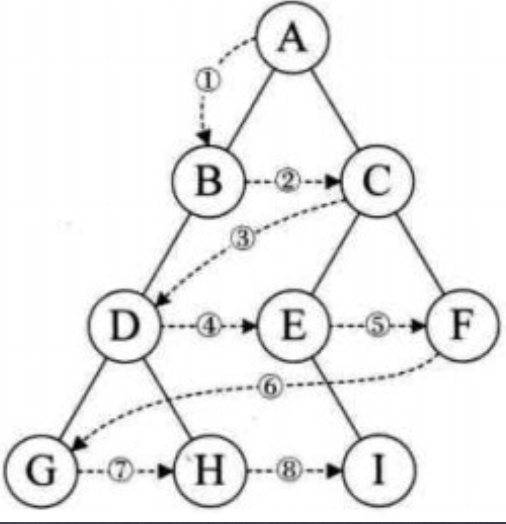
- 广度优先遍历(层序遍历)
核心
- 按照递归的思路
- 什么时候遍历到根节点
创建二叉树
//创建二叉树
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
function BST() {
this.root = null
}
BST.prototype.insert = function (data) {
var node = new Node(data, null, null);
if (!this.root) {
this.root = node;
} else {
function insertNode(root,node){
if(data< root.data) {
root.left === null ? (root.left = node) : (insertNode(root.left, node))
}else {
root.right === null ? (root.right = node) : (insertNode(root.right, node))
}
}
insertNode(this.root,node)
}
}
//测试数据
var bst = new BST();
var nums = [10,2,12];
for (let i = 0; i < nums.length; i++) {
bst.insert(nums[i]);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
先序遍历
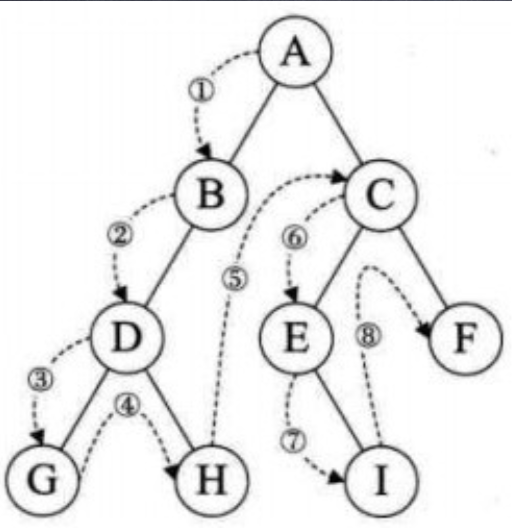
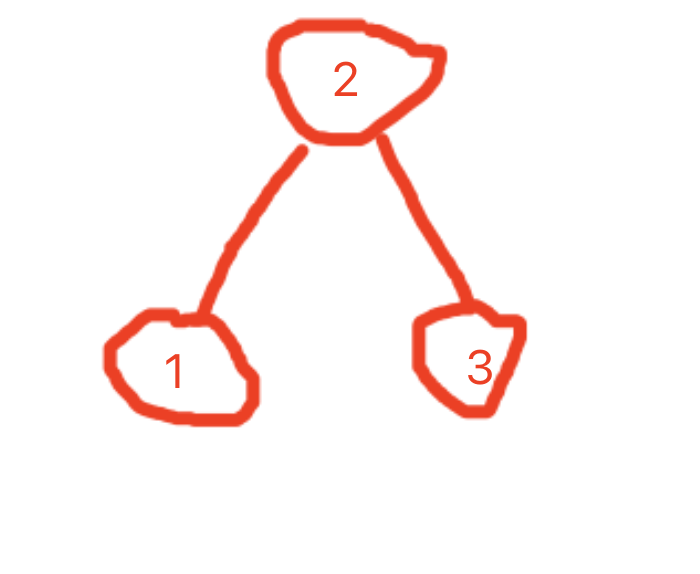
即根-左-右遍历,对于给定的二叉树根,从根节点开始。然后遍历左子节点i,如果i有左子节点一直递归遍历到最左边的叶子节点,而后遍历其右子节点,随着递归的逐渐出栈,遍历到最右边的叶子节点,最终完成遍历。
代码实现
//递归实现
var arr = []
function preorder(node){
if(node){
arr.push(node.data)
preorder(node.left)
preorder(node.right)
}
}
//非递归的
let dfs = function (nodes) {
let result = [];
let stack = [];
stack.push(nodes);
while(stack.length) { // 等同于 while(stack.length !== 0) 直到栈中的数据为空
let node = stack.pop(); // 取的是栈中最后一个j
result.push(node.value);
if(node.right) stack.push(node.right); // 先压入右子树
if(node.left) stack.push(node.left); // 后压入左子树
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
从根节点开始。
中序遍历
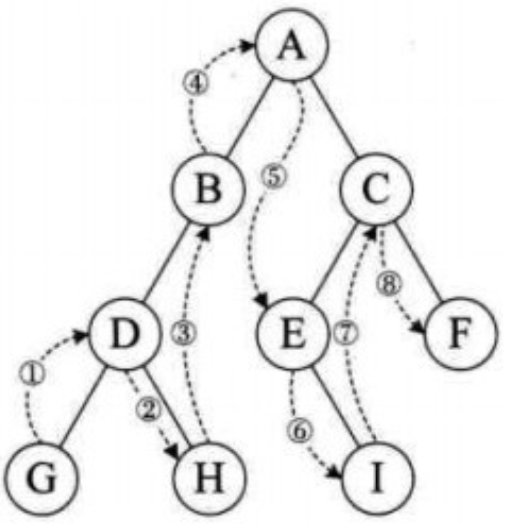
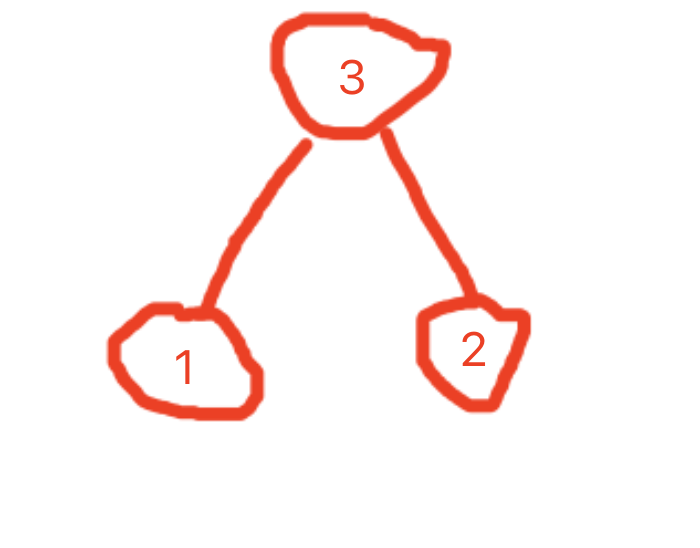
即左-根-右遍历,对于给定的二叉树根,从最左边的叶子节点开始。然后父节点i,再遍历i的右子节点,在遍历i(i 必然是其父节点的左子节点)的父节点,再遍历父节点的右子节点,随后遍历父节点的父节点,直到遍历到根节点后,遍历右子树的最左边的节点,随着递归的逐渐出栈,遍历到最右边的叶子节点,最终完成遍历。
实现代码
//递归实现
var arr = []
function preorder(node){
if(node){
preorder(node.left)
arr.push(node.data)
preorder(node.right)
}
}
//非递归的
let dfs = function (nodes) {
let result = [];
let stack = [];
while(stack.length || node) { // 是 || 不是 &&
if(node) {
stack.push(node);
node = node.left;
} else {
node = stack.pop();
result.push(node.value);
//node.right && stack.push(node.right);
node = node.right; // 如果没有右子树 会再次向栈中取一个结点即双亲结点
}
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
后序遍历
从最左边的叶子节点开始。
即左-右-根遍历,对于给定的二叉树根,从最左边的叶子节点开始,然后遍历其兄弟节点,然后遍历其父节点i,再遍历i的右子节点,再遍历i的父节点,直到遍历到根节点的左子节点(即根节点的左子节点遍历完后),再遍历右子树的最小层的最左边的节点,随着递归的逐渐出栈,遍历到根节点,最终完成遍历。
实现代码
//递归实现
var arr = []
function preorder(node){
if(node){
preorder(node.left)
arr.push(node.data)
preorder(node.right)
}
}
//非递归
function dfs(node) {
let result = [];
let stack = [];
stack.push(node);
while(stack.length) {
// 不能用node.touched !== 'left' 标记‘left’做判断,
// 因为回溯到该结点时,遍历右子树已经完成,该结点标记被更改为‘right’ 若用标记‘left’判断该if语句会一直生效导致死循环
if(node.left && !node.touched) { // 不要写成if(node.left && node.touched !== 'left')
// 遍历结点左子树时,对该结点做 ‘left’标记;为了子结点回溯到该(双亲)结点时,便不再访问左子树
node.touched = 'left';
node = node.left;
stack.push(node);
continue;
}
if(node.right && node.touched !== 'right') { // 右子树同上
node.touched = 'right';
node = node.right;
stack.push(node);
continue;
}
node = stack.pop(); // 该结点无左右子树时,从栈中取出一个结点,访问(并清理标记)
node.touched && delete node.touched; // 可以不清理不影响结果 只是第二次对同一颗树再执行该后序遍历方法时,结果就会出错啦因为你对这棵树做的标记还留在这棵树上
result.push(node.value);
node = stack.length ? stack[stack.length - 1] : null;
//node = stack.pop(); 这时当前结点不再从栈中取(弹出),而是不改变栈数据直接访问栈中最后一个结点
//如果这时当前结点去栈中取(弹出)会导致回溯时当该结点左右子树都被标记过时 当前结点又变成从栈中取会漏掉对结点的访问(存入结果数组中)
}
return result; // 返回值
}
dfs(tree);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
层序遍历(广度优先遍历)
对于给定的二叉树根,从根节点开始,遍历下一层的所有节点从左往右,然后又遍历下一层,随着递归的逐渐出栈,遍历到最右边的叶子节点,最终完成遍历。
应用:react的domdiff就是用的广度优先遍历,时间复杂度是O(n),最多遍历到O(1),但是如果遍历围棋这种东西的话,千万不要用,需要遍历360!实在太多了,所以使用深度优先。
const data = [
{
name: 'a',
children: [
{ name: 'b', children: [{ name: 'e' }] },
{ name: 'c', children: [{ name: 'f' }] },
{ name: 'd', children: [{ name: 'g' }] },
],
},
{
name: 'a2',
children: [
{ name: 'b2', children: [{ name: 'e2' }] },
{ name: 'c2', children: [{ name: 'f2' }] },
{ name: 'd2', children: [{ name: 'g2' }] },
],
}
]
实现代码
function ceng(data) {
var result = [];
var queue = data;
// 运用队列的知识解决
// 每次遍历当前的data
while (queue.length > 0) {
[...queue].forEach(ele=>{
queue.shift();
result.push(ele.name)
ele.children && queue.push(...ele.children)
})
}
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 树的实现
通过链式实现,在储存的时候可以把树按照一种规则存到线性表里
# 树的衍生
- 无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树 ,
- 有序树(二叉查找树或二叉搜索树):树中任意节点的子结点之间有顺序关系(缺点:有可能退化为线性链) 1.任意节点左子树不为空,则左子树的值均小于根节点的值 2.任意节点右子树不为空,则右子树的值均大于于根节点的值 4.任意节点的左右子树也分别是二叉查找树 3.没有键值相等的节点)
- 二叉树:每个节点最多含有两个子树的树称为二叉树
- 完全二叉树:除了最后一层,其它各层节点数都达到最大
- 满二叉树:每一层上的结点数都是最大结点数
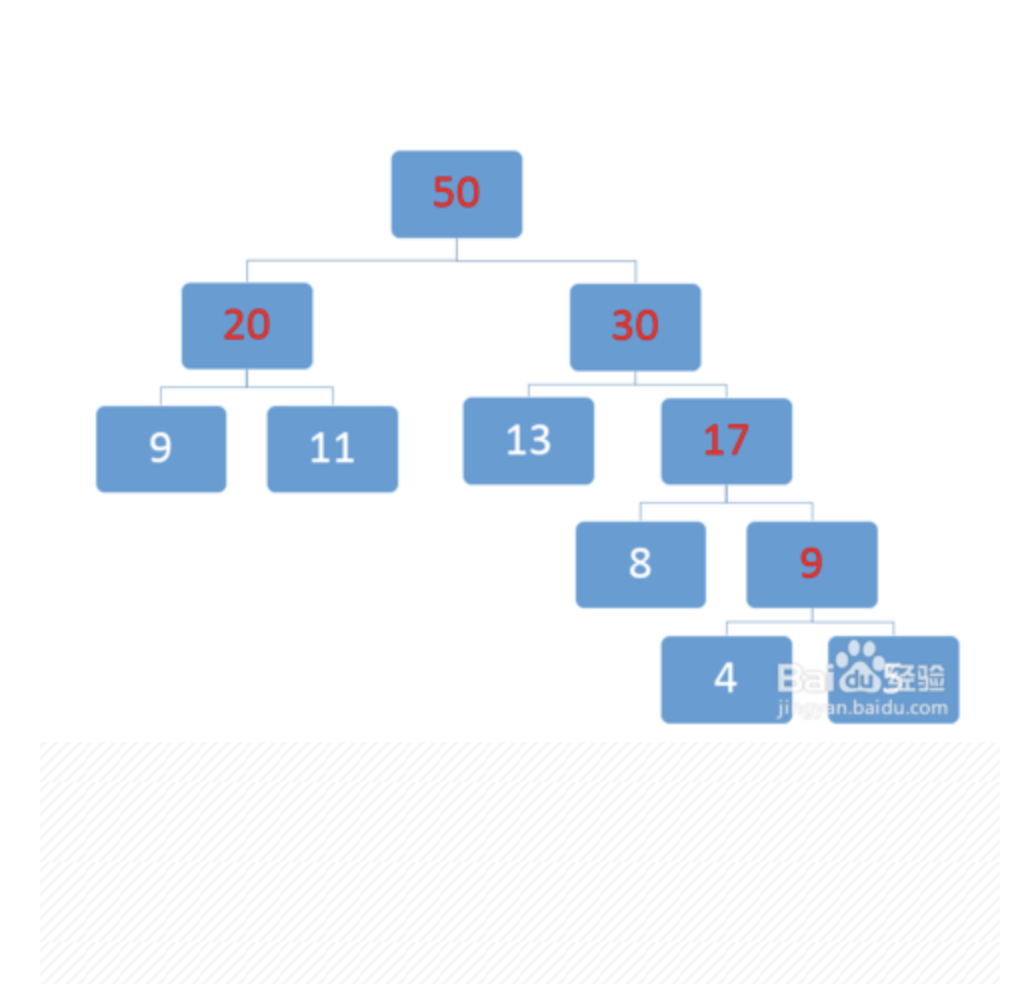
- 霍夫曼树:带权路径最短的二叉树,也叫最优二叉树,一般用来减少程序整体运行时间的,讲权重大的放在前边。
# 图
概念: 在计算机科学里,一个图就是一些顶点的集合,这些顶点通过一系列边结对连接。它是一种多对多的关系,没有空图的概念。
顶点:代表对象边:连接顶点与顶点,建立起对象之间的关系或关联权有向图与无向图:有向图就是按照一个方向走,无向图没有方向的概念。
# 按存储结构分类
存储结构分四类:顺序存储、链接存储、索引存储 和 散列存储。
- 顺序结构和链接结构适用在内存结构中。
- 索引结构和散列结构适用在外存与内存交互结构。
# 顺序存储
在计算机中用一组地址连续的存储单元依次存储线性表的各个数据元素,称作线性表的顺序存储结构。就比如一维数组
特点:
1、随机存取表中元素(有下标)。
2、插入和删除操作需要移动元素。
# 链接存储
在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。它不要求逻辑上相邻的元素在物理位置上也相邻.因此它没有顺序存储结构所具有的弱点,但也同时失去了顺序表可随机存取的优点。(像链表一样)
特点:
- 1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成,所以相同空间内假设全存满的话顺序比链式存储更多)。
- 2、逻辑上相邻的节点物理上不必相邻。
- 3、插入、删除灵活 (不必移动节点,只要改变节点中的指针)。
- 4、查找结点时链式存储要比顺序存储慢。
- 5、每个结点是由数据域和指针域组成。
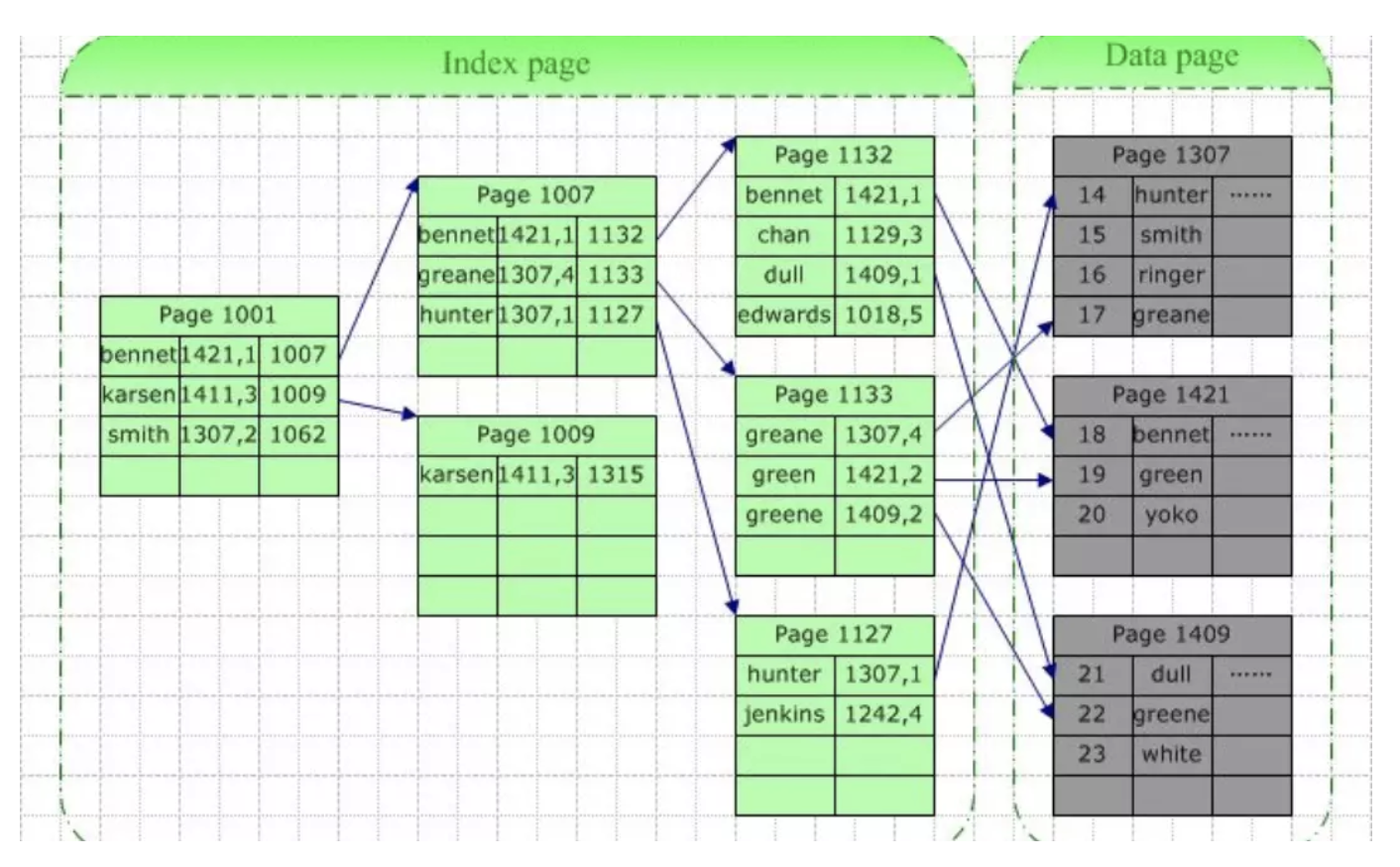
# 索引存储
除建立存储结点信息外,还建立附加的索引表来标识结点的地址。索引表由若干索引项组成。
除建立存储结点信息外,还建立附加的索引表来标识结点的地址。索引表由若干索引项组成,如果每个节点在索引表中都有一个索引项,则该索引表就被称为稠密索引。若一组节点在索引表中只对应于一个索引项,则该索引表就成为稀疏索引。索引项的一般形式一般是关键字、地址。在搜索引擎中,需要按某些关键字的值来查找记录,为此可以按关键字建立索引,这种索引就叫做倒排索引(因为是根据关键词来找链接地址,而不是通过某个链接搜索关键词,这里反过来了,所以称为倒排索引),带有倒排索引的文件就叫做倒排索引文件,又称为倒排文件。倒排文件可以实现快速检索,这种索引存储方法是目前搜索引擎最常用的存储方法。
存储单词的过程:先在某个地址空间存储单词,然后把该单词的关键词和存储地址存到附加的索引表。
查找某个单词的过程:先根据关键词找索引表,得到数据存储地址。然后再通过存储地址得到数据。
特点:
索引存储结构是用结点的索引号来确定结点存储地址,其优点是检索速度快,缺点是增加了附加的索引表,会占用较多的存储空间。
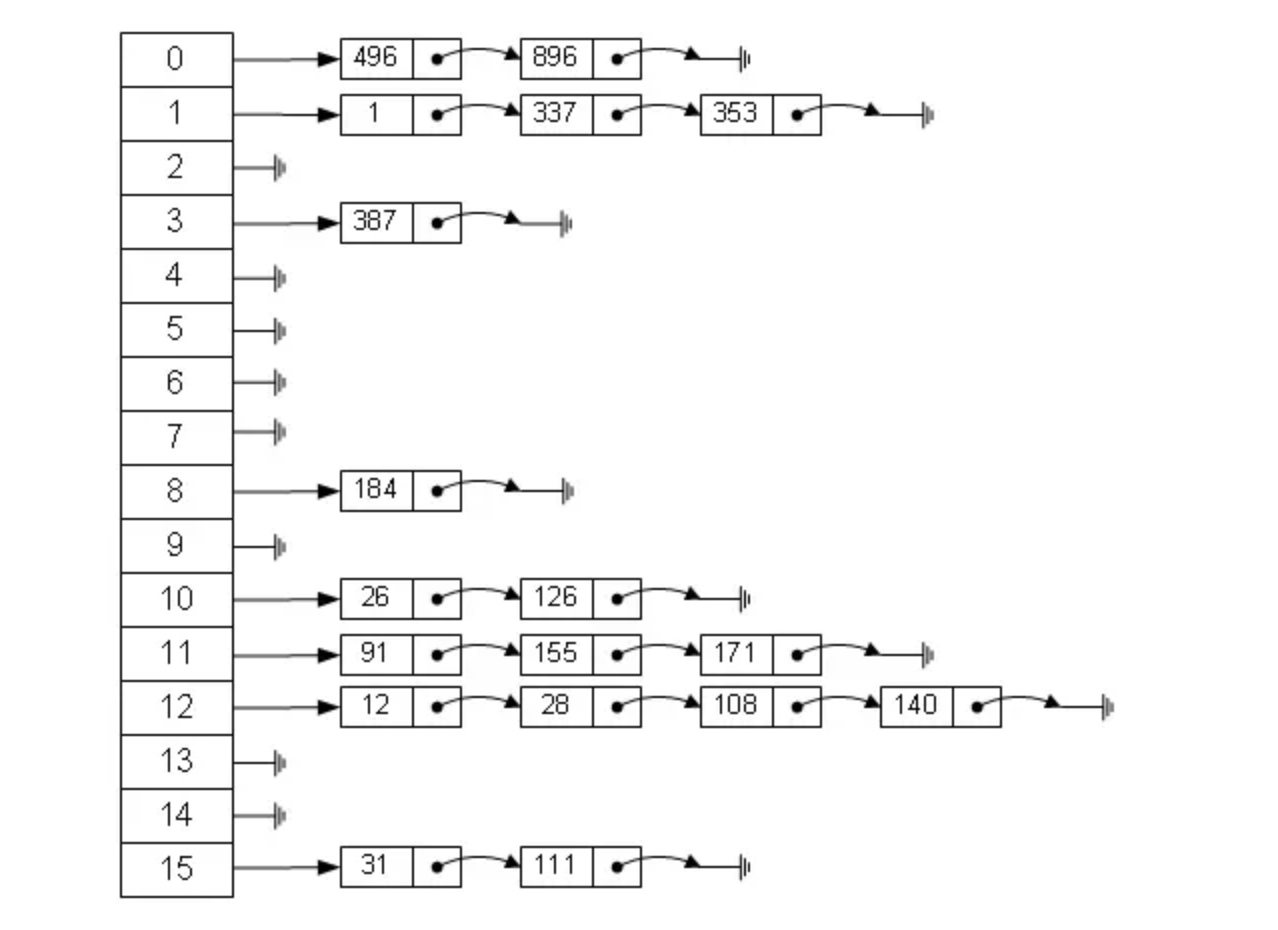
# 散列存储
散列存储,又称hash存储,是一种力图将数据元素的存储位置与关键码之间建立确定对应关系的查找技术。
散列法存储的基本思想是:由节点的关键码值。 散列法存储的基本思想是:它通过把关键码值映射到表中一个位置来访问记录(决定节点的存储地址),以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表,散列技术除了可以用于查找外,还可以用于存储。
特点:
散列是数组存储方式的一种发展,相比数组,散列的数据访问速度要高于数组,因为可以依据存储数据的部分内容找到数据在数组中的存储位置,进而能够快速实现数据的访问,理想的散列访问速度是非常迅速的,而不像在数组中的遍历过程,采用存储数组中内容的部分元素作为映射函数的输入,映射函数的输出就是存储数据的位置,这样的访问速度就省去了遍历数组的实现,因此时间复杂度可以认为为O(1),而数组遍历的时间复杂度为O(n)。
# 什么是算法
算法(algorithm),在数学和计算机科学之中,为任何良定义的具体计算步骤的一个序列,常用于计算、数据处理和自动推理。精确而言,算法是一个表示为有限长列表的有效方法。算法应包含清晰定义的指令用于计算函数。
- 算法不是数学,但是可以用数学来描述
- 我们要做一件事情,这个过程本身就是算法
- 我们最常用的增删改查是算法的一部分
- 算法可以用自然语言、流程图、伪代码和计算机语言等手段来表示
- 在面向对象语言中,算法通常通过类的方法实现
# 算法的特征
- 有穷性:算法必须能在执行有限个步骤之后终止
- 确切性:每一步骤必须有确切的定义
- 输入项:有0个或多个输入,用来规定初始情况,所谓0个输入是指算法本身定出了 初始条件
- 输出项:有一个或多个输出,是对输入数据处理后的结果。没有输出的算法毫无意义
- 可行性:算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步,每个计算步都可以在有限时间内完成(也称之为有效性)。
# 算法分类
算法可以分为以下几类:
分治法
- 递归(式),将大问题分解成子问题(子问题相互独立,且与原问题相同)、合并(将子问题得解合并成原问题的解)。
动态规划法
- 递归,记录已解决的子问题的答案,根据子问题求解原问题的解(子问题不独立)。
贪心算法
- 局部最优,根据当前信息做选择。(花钱找钱)
回溯法(暴力法)
- 通用的解题法,解空间树(深度优先遍历),找出满足条件的所有解。
- 枚举算法
分支界限法
- 解空间(广度优先、最小耗费优先)、界限函数(队列式、优先队列式)。
概率算法
- 随机性选择,小概率错误(运行时间大幅减少),对同一问题求解两次,可能得到完全不同的解,且所需时间、结果可能会有相当大的差别。
近似算法
- 求近似解,定义容错界。
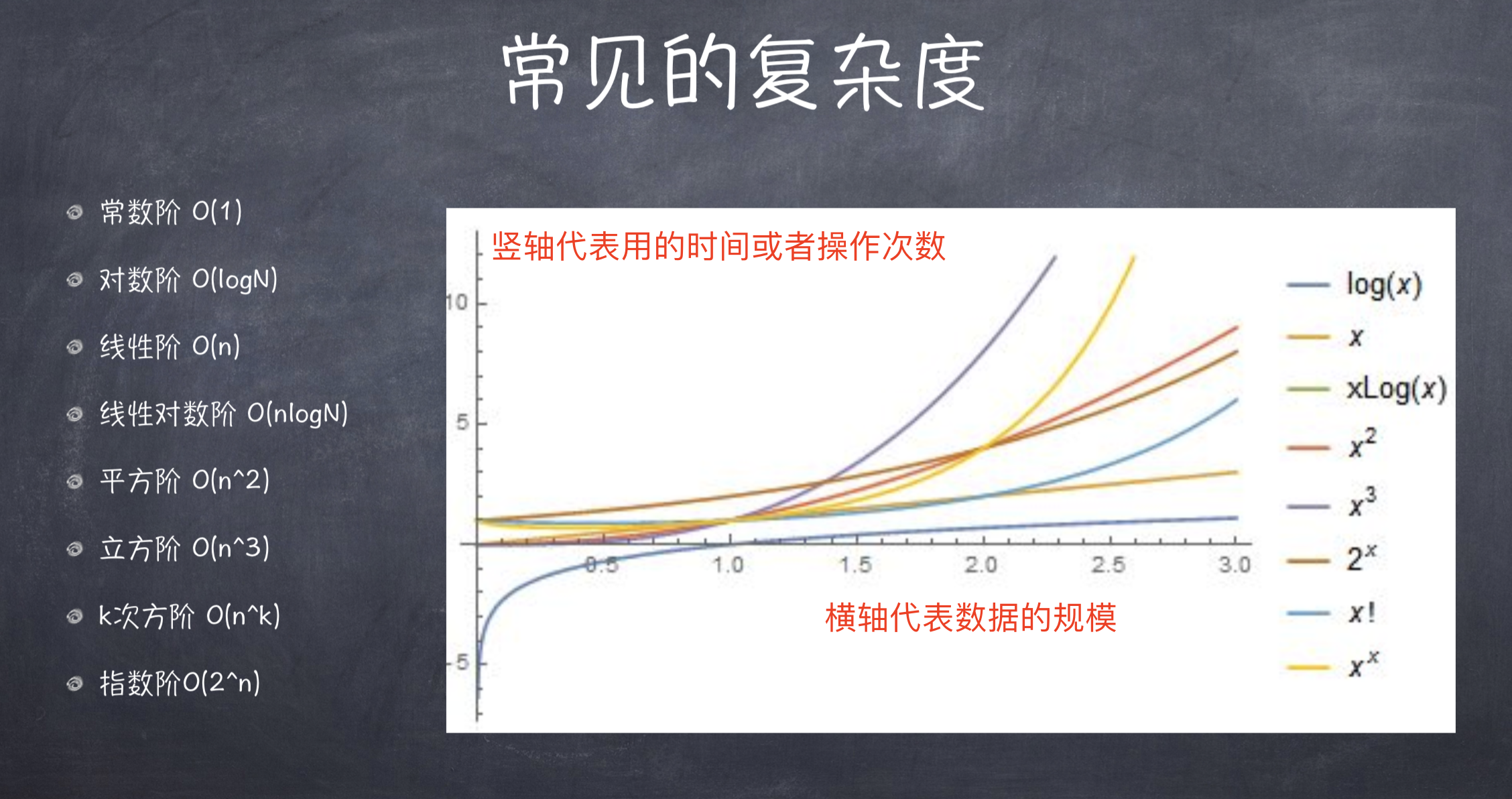
# 衡量算法的好坏
O(1),哈希查找。
O(n),单层循环。
O(lgn),二分法。将一个数据集分成两半,然后将分开的每一半再分成两半,依此类推。
O(nlgn),归并排序。将一个数据集分成两半,然后将分开的每一半再分成两半,依此类推,在此过程中同时遍历每一半数据。
O(n²),双重循环。
O(n³),三层循环。
O(2^n),穷举查找,检查所有子集。
O(n!),菲波那切数列。
2
3
4
5
6
7
8
图形越陡数据规模越大 从上图可以看出,常数阶是最好的,指数阶是最差的
空间复杂度
简单点说就是用的内存多少,或cpu,也就是对一个算法在运行过程中临时占用存储空间大小的量度。
正确性
想要的结果是正确的
可读性
让别人可以验证,可以看懂。
健壮性
# 如何计算算法的复杂度
- 随着问题规模 n 的不断增大,时间复杂度不断增大,算法的执行效率越 低。
- 一般做算法复杂度分析的时候,遵循下面的技巧: 有几重循环,一般来说一重就是O(n),两重就是 O(n^2),以此类推 如果有二分,则为O(logN)
- 保留最高项,去除常数项
# 基本算法
- 枚举
- 递归
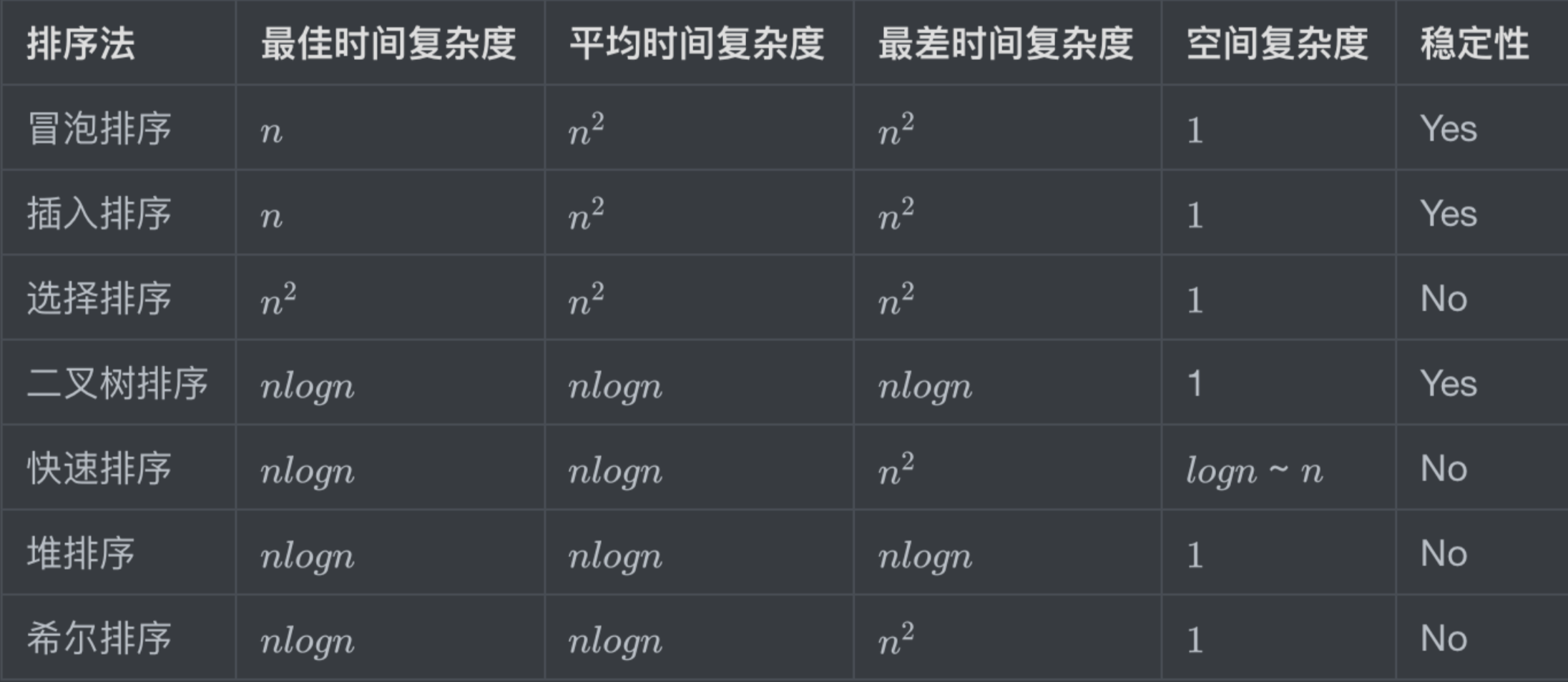
- 基本排序
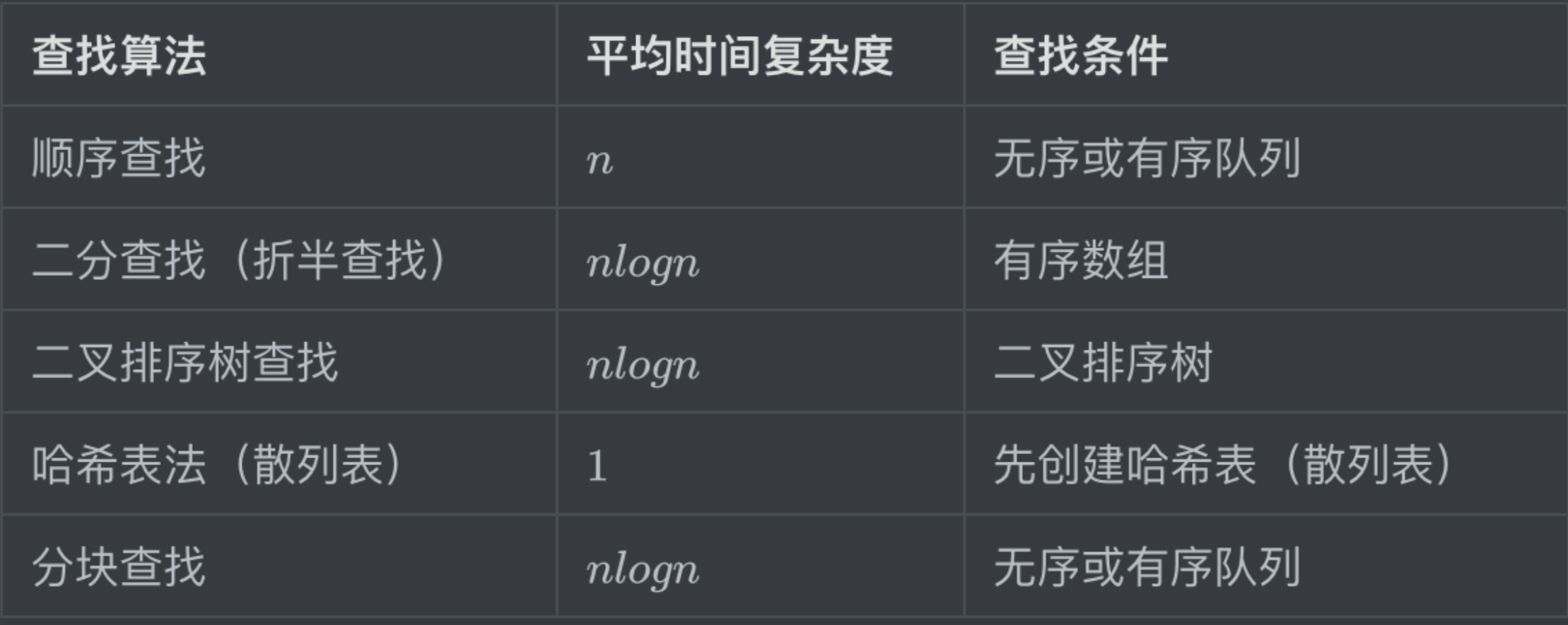
- 基本查找
# 枚举算法
核心思想:
枚举所有的可能。 本质:就是从所有候选答案中去搜索正确的解,使用该算法需要满足两个条件
- (1)可预先确定候选答案的数量;
- (2)候选答案的范围在求解之前必须有一个确定的集合。
特点:
枚举算法简单粗暴,暴力的枚举所有可能,尽可能地尝试所有的方法。 速度可能很慢,却是我们最应该优先考虑的。 实现最简单,并且得到的结果总是正确的。
# 递归算法
核心思想:
通过重复将问题分解为同类的子问题而解决问题的方法。
特点:
- 函数可以通过调用自身来进行递归
- 递归可以完全取代循环
递归由下面两部分组成:
- (1)递归主体,就是要循环解决问题的代码
- (2)递归的跳出条件,递归不能一直递归下去,需要完成一定条件后跳出
排序算法
查找算法
# 算法解题思路
当我们在遇到一个算法的问题时,可以按照以下步骤进行思考,避免走弯路。
- 枚举法:先不考虑算法复杂度,先用枚举法(暴力法)完成需求。
- 想办法优化,例如猜生日算法:
- 穷举法,从 1 月 1 日开始比对,比对到 12 月 31 日。要比对 366 次。
- 优化 1:先比对 12 次月份,确定完月份,再比对日期,最多要比对 12 + 31 次。
- 优化 2:使用二分法,先比对 6 月是大是小,确认完月份以后,再用同样的方法比对日期。
- 递归算法
- 化繁为简:将一个大事情,分解成 1 步 1 步的小事情。
- 分而治之:把问题分成多个模块,一块一块的解决。
- 化虚为实:将不明白的业务,转换成我们熟悉的业务,先理清逻辑,然后再替换回去。
# 如何养成算法思维
- 化繁为简
- 很难在第一时间内得到正确的思路的,这时候可以尝试一种由简至繁的思路。首先把问题规模缩小到非常容易解答 的地步。用来解决动态规划问题
- 分而治之
- 把问题分为两半,变成两个与原来问题同构的问题
- 当尝试这种思路时,其实只需要考虑两个问题:
- 1.一分为二以后,问题是否被简化了?
- 2.根据一分为二的两个问题的解,能否方便地得出整个问题的解?
- 化虚为实
- 使用另外一种形式进行替换